As far as I can tell, there are five basic qualities one has to be concerned about for your warship of space: (or Space! even)
How hard it hits
How many hits it can take
How accurately it fires
How fast it can move
How much it can carry
Pretty much any spaceship can be described with those variables. A dreadnought hits hard and takes a lot of hits but it moves very slowly. A transport also moves slowly, but it doesn't hit hard and carries a lot. A fighter moves quickly, but it doesn't hit very hard and I wouldn't bother insuring it.
Now, we need actual numbers to answer those questions, but those are hard to provide. I can't tell you how hard something hits without being able to make statements about how many hits ships take. I can't tell you how fast it can move without going over how much it can carry, and whether it's empty or full. And I can't make any statements about any of that without answering all kinds of questions about the underlying technology; what kinds of engines the ships use, how much reaction mass they're toting around, how large you can make a Langston field, how many crew are necessary to run a ship and how effective is the life support, that sort of stuff.
Well, I'm going to start answering some questions, if only in a generic, background sort of way. To start with, how do the ships move in space? Last time I spoke about this, I was talking of interplanetary travel, not the short bursts of hard acceleration that are preferable in combat.
The first thing to understand about movement in space is that there's no air resistance. There's no friction, and nothing that will slow you down. As long as you keep your rocket firing, you'll keep accelerating, at least until you hit relativistic concerns. The most important implication is that you have no polite way to stop, other than by shoving even more reaction mass forward. You accelerate halfway there, you decelerate halfway back. Ok, we covered that already, at least for interplanetary trips.
On the other hand, if you're in mid combat, well, that isn't going to cut it. You want to be able to move any which way at a moment's notice. So you need a way to keep track of how you've been moving. Enter the vectors.
What's a vector? It's the word they use for something that carries a disease. In a definition more germane to the task at hand, mathematically it's any quantity that has a direction and a size. Velocity and acceleration comprise our vectors of choice. Here I'm going to be borrowing heavily from the board game Triplanetary. From the inestimably valuable Project Rho we get a description of the movement rules, which are really the most interesting part of the game.
Basically, you preserve whatever motion you had last turn, and you can add on one space of acceleration in any direction to change that vector. Suppose you're going left at two hexes a turn. If you want to speed up you can accelerate in the direction you're moving and next turn you'll be coasting along at three hexes a turn. Or if you want to stop you can accelerate directly opposite the direction you're moving and you'll be going one hex a turn next turn, and can stop further from there. Or if you want to curve, well, you can modify your movement vector that way.
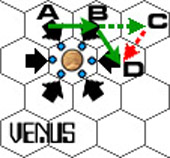
The real fascinating bit, and the part that got me to shell out for my own copy of the game, is how the game handles orbits: as a natural consequence of the simple rules the game allows you to park your ships spinning around a planet with no expenditure of fuel. Exactly like real life. If you want the details, I highly suggest you click over to Project Rho and read about it yourself--I'm not going to recap it here.
The only trouble is that you're stuck with a fixed number of gravity hexes. Imagine you wanted to draw a gravity arrow mid hex C. It'd point directly at the planet, but unfortunately not directly at another hex. You'd screw up your movement going through there as you wouldn't land in the middle of another hex. So if I want to make other, interesting battlefields I can't use the system as is. Especially since I want ships to accelerate at different speeds. You can't move in fractional hexes, so you'd have to have your faster ships move more hexes, which diminishes the value of a block of six gravity hexes; it's too easy to go around.
If I was laying the battle out on a physical board then I doubt I could come up with a better system than Triplanetary runs. On the other hand, why am I constraining myself to a physical board? I'm not going to make it into a video game, but there are advantages to going part way. Let's say we keep time discrete, measured in units of turns, but make space continuous. (As a side note, most video games don't even go there. They make time and space both discrete, or both continuous). What does that do for us?
To start with, it neatly solves the problem of fractional hexes, by allowing fractional hexes. This in turn allows much more flexibility in constructing gravity fields for the ships to fight in. Imagine, for example, a large and long rectangle, with Mars forming the lower right corner. The closer your spaceships get to Mars, the larger effect gravity has on their movements. On the other side of the board though, there isn't much effect at all. But since we're letting the computer worry about it we can still factor it into the result. It also allows fractional movement. Different ships can have different accelerations and still be neatly included on the board without having to worry about it.
The computer also allows us to dynamically track distances and odds. If I'm accelerating this way and I'm at that speed already, how likely am I to hit that guy doing similar things in other directions? If I were figuring this in Gary Gygax's basement forty years ago (has it really been that long?) I'd have to include formula and tables and whatnot, but again, we can let the computer worry about all that. We can even, at little extra cost of expenditure, figure out things like glancing blows (if a nuke detonates at this radius from a ship, how much energy is imparted to their shield?) and the effects of exploding ships on others in their radius. Wonderful stuff, really. I don't have the calculations mapped out yet, but I don't forsee them being too terrible. Or the programming, but that's another issue.
No comments:
Post a Comment